Is there a more divisive and combative conversation to have with a staff than the zero? Just ask the question, What should a student receive when they don’t submit their work? Let’s clarify, we’re talking about the zero on a traditional 100-point scale. For the purpose of this post, we’ll assume the traditional 10-point intervals in the 100-point scale. I am aware this varies wildly if you check schools, districts, or even states across the US.

I’ll begin by saying that many schools and districts have attempted to have this conversation, but some have back-pedaled when the explosion of deep emotions erupted across the school or district. The enemy here is not the zero. The enemy is the 100-point scale, and I’ll do my best to explain.

A zero on a 100-point scale is mathematically inequitable. The entire scale is too heavily weighted on the side of failure. When giving a 0, we actually give a student a score that is worse than failure.

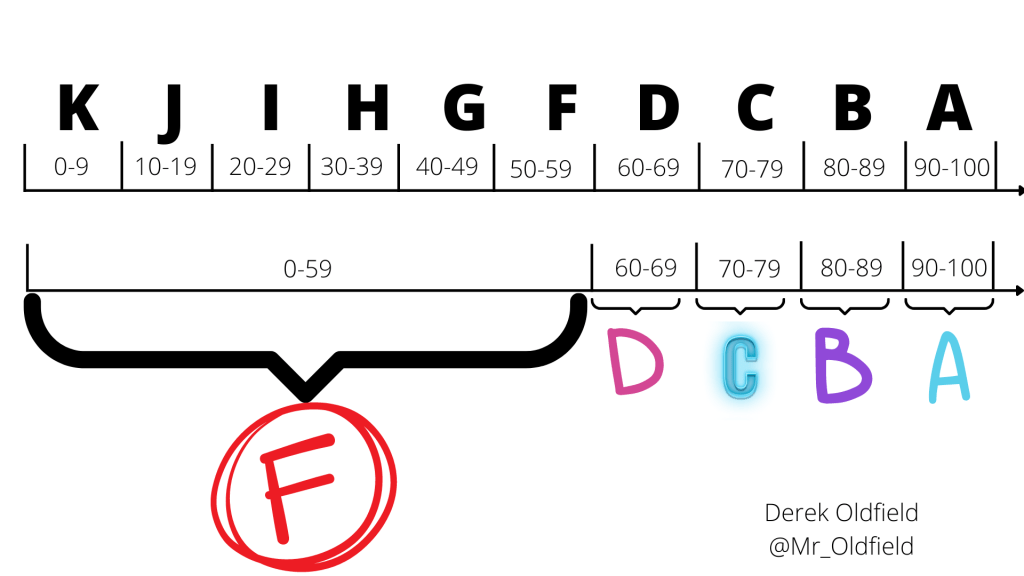
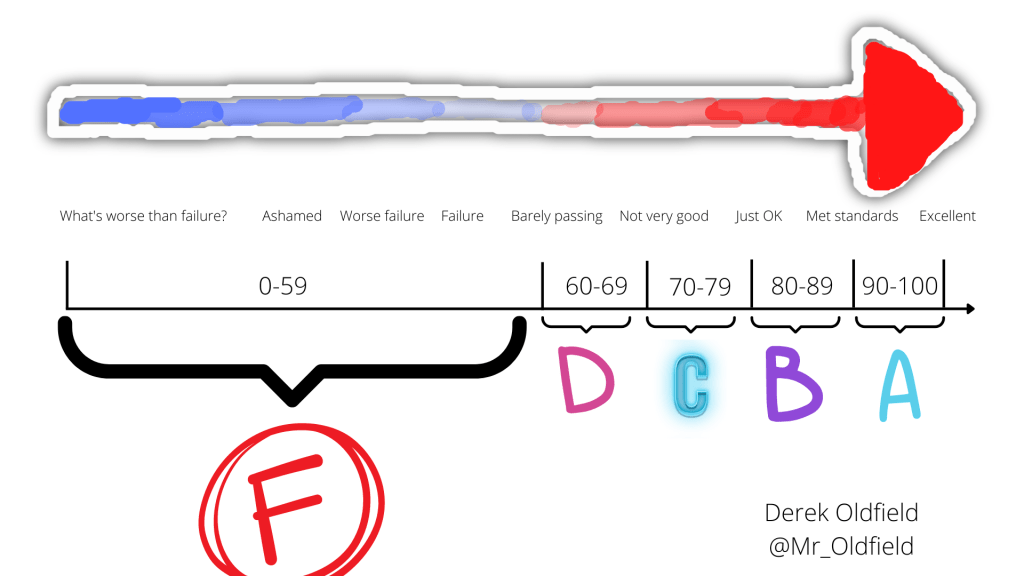
If you look at the images above, you can see equal intervals between the other letter grades, but there’s this huge gap when we get to F. We could argue over what an A means, what a B means, or what a C means, but let’s hold that for another post. Whatever your descriptors are, F has to mean failure. In the traditional 100-point scale, it would appear there are degrees of failure. Take these humble descriptors as an example:

The zero has an undue deflationary effect on a student’s overall average, the same way the scale would have an undue inflationary effect if we flipped it.

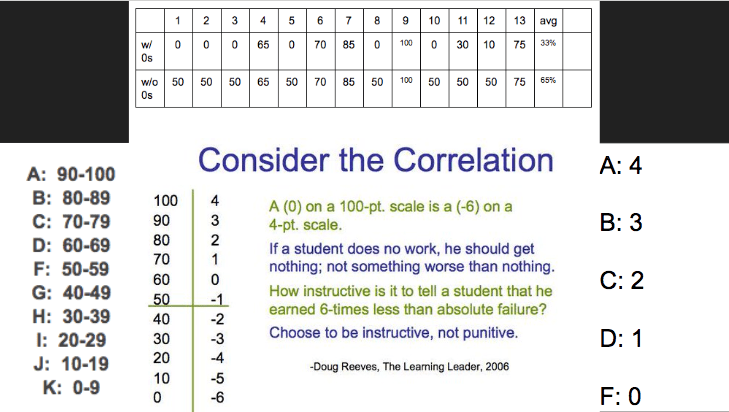
I’ve never seen a teacher give a student a 140 on a test. I imagine they would look at me sideways if I asked them why. Of course, a 140 would be an inaccurate score that would inflate the average of the grade. The zero on a 100-point scale is just as inaccurate and just as deflating to that average score. Let’s do an experiment.

As you see above, the student received a zero and after 11 additional 85s in the gradebook, the student still had not raised the grade back to a B. This is an example of the hole a zero places students in, and it represents the deflationary effect a zero has on the average. The student who received a zero has little motivation moving forward because their grade has been falsified by the impact of the zero.

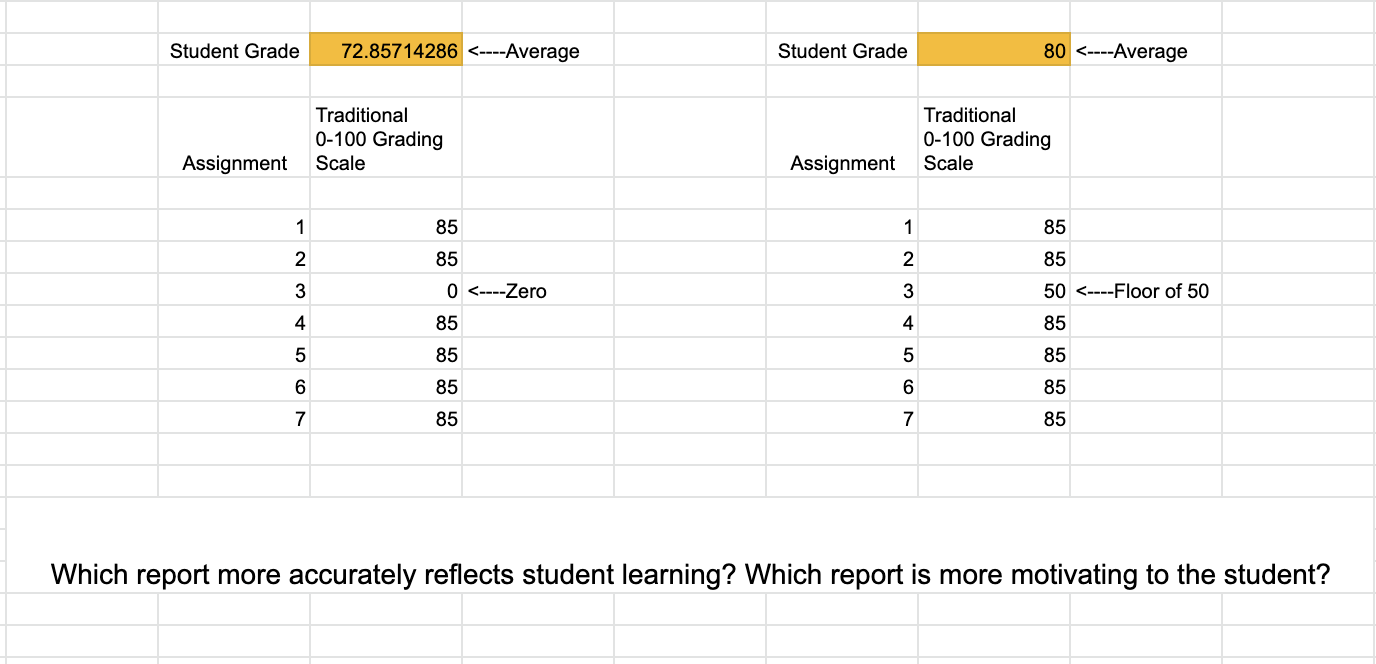
Let’s compare the effect of the zero versus establishing a floor of 50. Some schools or districts choose to use a 50 to represent missing work because the 50 maintains the equal intervals 100-90, 89-80, 79-70, 69-60, 59-50.

I appreciate the work of so many educators who influenced my thinking on this topic several years ago. Alexis Tamony created a wonderful YouTube video where she displays and discusses this very topic and I appreciate her influence on this post. Despite the evidence presented, I’m not naive. This is still a hard philosophical pill to swallow. I recommend schools and districts seriously consider moving to a scale where a zero makes sense. We use a 4-point scale to calculate GPA, for example. An A is worth a 4, B is a 3, C is a 2, D is a 1, and F is a 0. In this scale, educators could use zeroes that make sense. There are plenty of conversion charts out there if you feel the need to convert these to percentages. The use of percentages are primarily used to rank and sort students. Are there additional advantages to using a smaller scale? Yes! Inter-rater reliability increases dramatically when using a smaller scale. Think about it, can a human really discern learning to 101 different levels (0-100)? No. Can you really communicate the difference between a 78 and an 82?

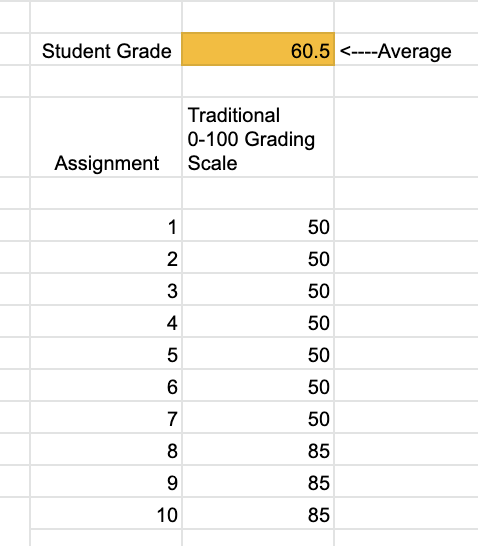
There also seems to be this fear among some educators that if we establish a floor of 50, some students might do nothing until the end of the grading period where they turn in 2-3 assignments and suddenly they have a passing grade. Here’s an example:

The student had ten scores during the grading period and seven of those were a 50 for missing or deficient work. You see the student submitted three assignments and scored an 85 on those three, which has raised the average to a 60.5, barely a passing score (D) on the traditional 10-point intervals. This leads us to my final consideration. Measuring and communicating learning is very much a human act requiring professional judgment. Educators dismiss this act far too often by allowing computers and phony math to place the final declaration of learning on a student’s grade. As professionals, we should be using professional judgment anytime we place a grade. What would you do in this situation?