I use Khan Academy’s system of exercises in my classroom.  My students receive a blend of instruction via the feedback provided by Khan Academy exercises and face to face time in my classroom.  We typically spend 2 days a week in a computer lab setting and 3 days of the week in my classroom.  The time in my classroom is predominantly driven by what has occurred on Khan Academy.  This type of approach is referred to as blended learning.

I often rearrange the seating in my classroom to put students in the best possible position to succeed.  I don’t have assigned seats, but I like to keep it fluid and dynamic.  When we are in my classroom, I try to incorporate more task-based problems that require my students to develop and demonstrate a deeper understanding in order to complete.  I also try to keep my classroom student-centered.  My assistant principal recently completed an observation in my room and estimated that I did about 5% of the teaching and the students did the other 95%.  A lot of my preparation is designing lessons that allow students to collaborate, talk, and learn freely and from each other.  Often my classroom looks chaotic, but lend an ear to the conversation for a couple minutes and you’ll find that students are busy solving problems, communicating, and thinking.

Some days the data provided to me by Khan Academy dictates that I need to do more direct teaching.  Some days the data suggests that my students are ready for something tougher.  Often, the following actions may be on display simultaneously during class:

• 4-5 students are completing a paper/pencil assessment or a retake of a prior assessment
• 10-12 students are at the computers working on a variety of targeted and personalized exercises
• 3-4 students are walking around with dry-erase boards acting as support for the students who are working.

 

I don’t let the curriculum map influence my pace at all.  I used to be a slave to that map and I was constantly assessing whether I would make it through the end of the map by May.  Student learning came second to the emphasis I placed on getting to every topic by May.  I have completely let go of that and my students are benefiting.

During our parent-teacher conferences, I’m often asked “So just how do you use Khan Academy in your classroom?”

Recently my classes began a new section on Exponents.  The standard related to this material literally reads “I can use properties of integer exponents, including zero and negative exponents to evaluate and simplify numerical expressions containing exponents.”  The following standard reads “I am able to derive and explain the properties of exponents.”  During this section, I like to introduce the material at the computer lab using Khan Academy.  I’ll take my students to the lab and direct them to a specific exercise.  Below you’ll see an example of what a student may see during that day.  This particular exercise is very basic and allows the student to demonstrate a shallow, procedural level of knowledge related to that standard.  Quite simply, can students identify what to do when like-bases are divided?  Or multiplied?  Or when an exponent is raised to another exponent?

 

Keep in mind that this particular concept is very new to the students.  At this point, I haven’t introduced the concept at all.

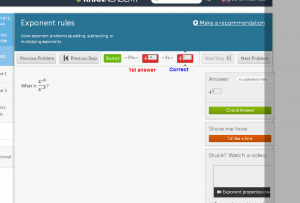
Pardon me while I try to step into the mind of a student seeing this problem for the first time.  I can imagine that they apply a bit of problem solving strategies here and simply try to apply something that comes to mind.  In the problem above, it appears this student tried to add the two exponents and Khan Academy told them to try again.  Three seconds later this student decided to subtract the two exponents and Khan Academy indicated to them they had arrived at the correct answer.   The very next problem can be found below.

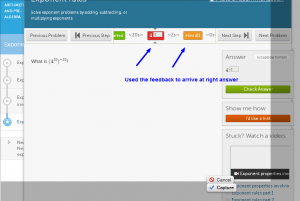This time the student decided that he should use a hint for help in solving this problem.  Of course, there is a very specific procedure that can be applied here when raising one exponent to another exponent, but the students have not yet learned this, nor have they had any instruction on the concept.  You can’t see it by looking at the screenshot, but this student used the hints and eventually used enough hints until the correct answer was given to him by Khan Academy.  So the student enters the correct answer and moves to the next problem.

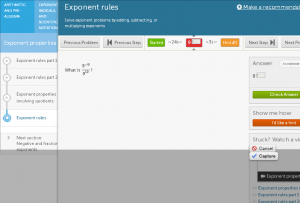
Skip ahead 12 problems and you see that this particular problem (see below) appears very similar to the one the student saw earlier.  You can also see that he needed to use the hints to help him arrive at the correct answer.  Apparently the student didn’t remember the feedback that was provided to him earlier.  This is typical at this point in the learning process.  Note that while using the hints, the student can stop asking for a hint at any point when he/she has seen enough to allow them to provide the correct answer.  If needed, they can ask for enough hints until Khan Academy gives them the answer.  Either way, Khan Academy doesn’t award credit for that answer when determining proficiency.  What you can see in the problem below is that this student hasn’t yet developed permanent recall of the specific rules; when to add the exponents, when to subtract the exponents, and when to multiply the exponents.  Earlier, the student employed his own problem solving strategies, but now you can see that he’s employing the hints in order to help learn the procedure in hopes that he can apply the correct procedure to a future problem.

What happens during a class period such as this one is the students begin to develop their own procedures, methods, and strategies for problem solving by using the feedback provided by the system.  Without much assistance from me, a number of students will actually correct their mistakes, use the feedback, the hints, or maybe even a video and in a 45 minute class period will actually get enough consecutive problems correct that Khan Academy will deem them proficient and classify them in a “practiced” level, indicating to me and the student that they have earned enough consecutive questions correct to be awarded that category.  On the other hand, those students who don’t earn this classification have still been introduced to the concept and provided enough feedback that they will come into class the following day with a better understanding than they had the previous day.  In fact, a number of those students will have partial understanding of the correct procedures.  For example, they may be able to correctly identify when to multiply the exponents, but are still shaky on when to add or subtract those exponents.  All of this is provided to me in a multitude of data.  Below you’ll see an example of class data available to me today, immediately after 2nd period.

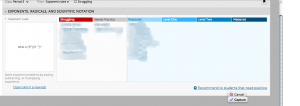Fast forward to tomorrow.  We’ll spend all class period in my room, not the computer lab.  At some point before class tomorrow I’ll review this screen again and determine which students have already demonstrated a level of procedural knowledge and which students haven’t.  The students who have demonstrated enough proficiency to earn that “practiced” level will most likely end up helping the other students iron out the wrinkles in their own procedures.  Students will be talking about what they tried in the lab and why it failed.  I’ll give students an opportunity to respond to the class about what a peer instructed them to do.  Whether they admit it or not, everyone has developed some procedure, but not everyone has the right one yet.  The students under the red column benefit because most of them will end the class period tomorrow feeling like a 3 or 4.  I employ a very simple informal assessment procedure where my students give me a 1-5 at the end of the period.  1 represents a student who feels lost.  3 represents a student who knows what to do but couldn’t teach it to anyone else yet.  5 represents a student who knows it so well they could teach it to someone else.  The students under the blue column benefit because the best way to retain information you have learned is to teach it to someone else.
What I’ve described to you has proved to me to be the quickest way to move students to that first, most basic, and most shallow level of understanding in a concept such as this.  Tomorrow in my class you’ll see me explaining to the students that x times x times x times x times x divided by x times x yields x^3 because two sets of x/x cancels to make 1.  We’ll use dry-erase boards to practice solving similar problems.  I’ll allow students to check answers while I check answers.  Half of the period I’ll spend down on a knee next to a student or groups of students.  I may place a group of 5 students who appear under the red “struggling” column all at one table so I can focus my attention on those students.  I’ll give them problems like (4^?)(4^-8) = 4^5.  Students will apply previous concepts like 1/x^-3 = x^3 to help them solve problems that involve the quotient rule.  Together, with the help of the data provided to me by Khan Academy, the students and I will work to move everyone to that basic procedural knowledge of exponent rules.

In the upcoming days and into next week I’ll provide this class with activities that allow them to develop a deeper understanding of the concept, one in which they won’t forget.  After passing my assessment, students will be instructed to write a blog post deriving and explaining the properties of exponents.  Some students may choose to include a picture from their dry-erase board to help the reader understand their explanation.  Other students may choose to create a video of them instructing from the board in the front of my room.  Still, other students may exercise their strengths in writing to explain to the reader their understanding of the properties of exponents.